My research interests fall in the realm of dynamical systems and chaos in nonlinear systems, with particular focus on problems of chaotic transport, mixing and information theory. I am interested in applications of my research to various physical systems including chaos in classical atoms, single atom computing, fluid mixing and insect swarming.

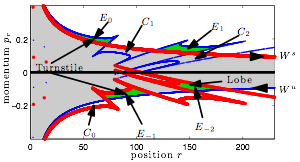
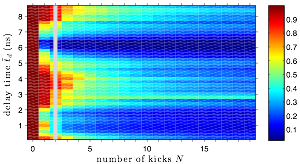
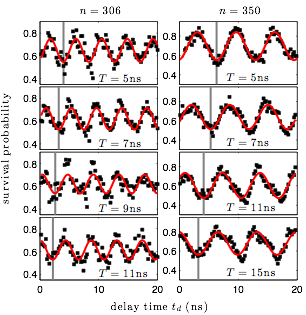
Chaotic ionization of bidirectionally kicked Rydberg atoms is governed by the turnstile portion of the homoclinic tangle. In order to experimentally observe the homoclinic tangle in this system, we measured the survival probability (a fraction of the electrons that do not ionize after application of the bidirectional kicks) of the electron ensemble orbiting the nucleus as a function of its position in state space. The oscillations in the survival probability are a direct signature of the overlap between the turnstile and the electron ensemble. You can read more about this experiment and the results here.

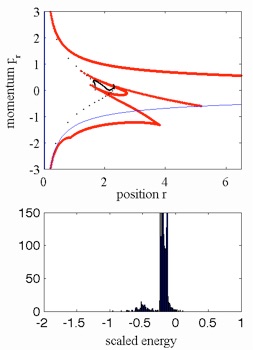
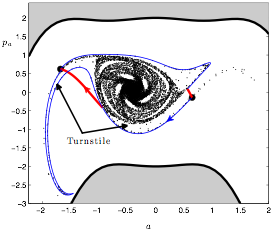
The homoclinic tangle organizes not only the ionization process, but also the full dynamics of the bidirectionally kicked Rydberg atoms. Thus, the homoclinic tangle can be exploited to quickly and efficiently change the energy of the electron ensemble. Sample results are shown in the figure. The top figure shows the electron ensemble in relationship to the turnstile portion of the homoclinic tangle, while the bottom figure shows the final energy in scaled units of the ensemble. The initial energy in this case was -0.5. (A paper on this topic coming soon.)

Another interesting chaotic atomic system consists of a hydrogen atom placed in external perpendicular electric and magnetic fields. My interest in this system comes from the fact that the global surface of section is yet to be computed. However, I have been able to calculate a local surface of section capable of capturing the turnstile as well as the existence of stable islands. (A paper on this topic is coming soon.)

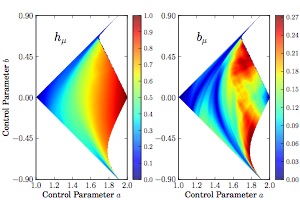
One of the main signatures of a chaotic systems is that it creates information. The rate of information creation is measured by system’s metric entropy. However, not all the information created is remembered by the system and the high rate of the information creation does not necessarily correspond to more remembered information. You can read more about those results here and their importance here. I am currently working on the physical interpretation of the remembered information since it is the crucial quantity in designing the most efficient chaos-based atomic computer.

I am interested in utilizing the tools commonly used in nonlinear dynamics, chaos theory and information theory to create novel chaos based systems. Chaotic systems are inherently sensitive to the change of both initial conditions and system parameters. This fundamental instability is typically viewed as an engineering challenge, requiring control mechanisms to tame the dynamics and give predictable outcomes. However, if handled carefully, chaotic dynamics can also be exploited to produce novel and counter-intuitive applications. A recent celebrated example is a chaogate, a logic gate that uses patterns generated by chaotic dynamics to transform input bits to the desired outputs. One of the unique and powerful capabilities of chaogates is that they can be reconfigured within a single clock cycle into any other logic gate. Thus, chaogates provide hardware-level programmability of circuit elements. Since the enhanced levels of security are embedded in the physical behavior of the system, chaogates are promising candidates for a new era of secure computing, and thus have a potential for a broad impact on society’s use of networked computing.

In principle, chaos-based logic gates can be implemented within any physical system exhibiting a sufficient level of chaos. Numerous “exotic” implementations have been proposed, but thus far realizations have been restricted to macroscopic nonlinear circuit elements. I am currently working on developing necessary theoretical foundation whose final goal is to use Rydberg atoms as a chaos-based computer.

We have all experienced the inability to hear and understand our conversation partner in a crowded room. The difficulty tends to be most apparent in a crowded bar or a club setting. I am interested in understanding the noise behavior in a crowded room. The noise level is usually not constant everywhere in the room and the transition from the quiet to noisy environment exhibits some very interesting behavior. Aside from being interested in problem that can cause some socially very awkward situations, I am also intrigued about the signal propagation in the presence of outside noise.

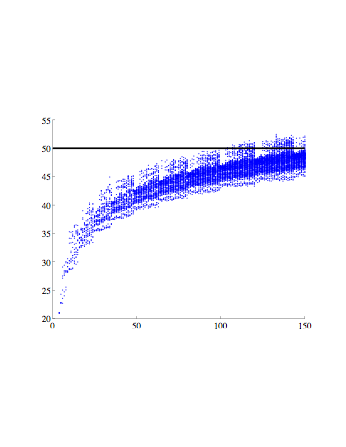
number of people in a small bar