Information Theoretic Approaches to Spiking Models
Developed for Physics 256 (taught by Jim Crutchfield)
Introduction
Motivation
The central nervous system is remarkable in its capacity to steer us through the world, juggling a massive scope of both physical and mental tasks, all of which are essential to the maintenance of our well being as well as to the success of our everyday and long-term endeavours. Implicit in the nominal operation of this network based biological machine is the capacity to accept, translate, store, and manipulate sensory information, ultimately allowing us to engage the environment around us in meaningful ways. The processes through which neural systems capture, code and use this information are of utmost importance to understand in the wider context of humanity's project to comprehend ourselves and the organisms from which we have evolved.
When modelling a system with billions of connected parts, each requiring possibly hundreds of variables in order to meet certain levels of accuracy, it can be daunting to know where to place one's focus. One such focus is on neural subsystems, small circuits of neurons modelled as visulizable networks with precisely defined connectivity. If it can be shown that such systems have functionality in their own right which can be utilized repeatedly by the larger system in which they exist, then it is not a far stretch to suggest that a comprehensive understanding of the computational and functional capacity of these subsystems is a key building block towards decoding the brain.
In this vein, I previously built a software tool with which to simplify the study of structure-function relationships in spiking neural network models. The interactive graphical interface allows a researcher to construct small to medium sized networks, modify connectivity and observe temporal response of the network to a full range of initial conditions. Until recently, all my behavioral observations of networks running on this system have been qualitative as have been my conclusions.
Having made these and other coarse qualitative observations, I sought in the current project to begin to characterize in a quantitative fashion the range of behaviors possible in spiking networks of various connectivity. Specifically, for small networks of six neurons, I have systematically examined and compared entropies in the behavior of networks with a range of connectivity patterns and noted trends in the types of spike patterns with which these entropies are correlated. Addtionally, I have studied mutual information between spike trains of individual neurons in small networks and made conclusions regarding how structural connectivity may be reflected in such behavioral measurements.
Synopsis of project and results
The current work presented here makes two broad contributions to the study of the structure and flow of information in spiking neural networks:
- Entropy was calcuated, maximized and correlated to behavioral patterns of a particular class of six node spiking neural networks. The specific finding here is that entropy maximization could consistently be characterized as following one of two strategies. Either (1) networks produced spike bit streams containing a large number of different patterns with variable probability density function shapes or (2) networks produced a few patterns which appeared almost with uniform probability. As will be shown below, both of these strategies work to maximize entropy. Interestingly, in my observation, 6 node networks of this variety were unable to employ both strategies simultaneously.
- Shifted mutual information was tabulated between all pairwise combinations of neurons and temporal shifts of four time steps or more, forwards and backwards. Loosely such a quantatative measure informs us of the degree to which a spike train recording of one neuron may be indicative of what to expect in the recording of another neuron. The temporal shifting gives us a sense of the temporal relationship between the two neurons. Intuitively one might expect that the behavior of a neuron which stimulates another neuron should be informative of the latter neuron's behavior. This finding is verified and explored further in context of the well known "data processing inequality" of Markov chains.
Background
Neurobiology and information theory
Neural networks connect the worlds of neurobiology, mathematics and computer science. In short they are simplified mathematical models which try to capture essential properties of neurobiological systems in order to either understand such systems or use the inherent capabilities within them to do useful computation. An abbreviated introduction with links to more substantial sources can be found here.
Recent studies focusing on the computational capabilities of neurobiological networks have suggested that information may often be encoded in a more precise way than can be represented by a perceptron-like artificial neural networks. The latter sort of model employs a spike rate representation of a neural spike train, smearing the timing of individual spikes in the underlying biological system. Several studies have found that temporal resolutions of neural codes are on a millisecond time scale, which highlights the significance of the precision of spikes in the coding process.
Recent years have also seen considerable progress in using information theoretic methods to address the structure of the neural code. These approaches present a scientist with the capability to quantify responses to arbitrarily complex stimuli. Measurements of entropy and information in spike trains have been used previously to test the hypothesis that neural codes adapt to sensory input distributions and optimize efficiency and speed of information transmission.
Previous Work
Previously I built a software tool with which to investigate the activity of spiking neural networks across a range of topologies. Specifically, I was interested in studying the compelling information-rich activity which emerges in a transition regime between quiescence and constant saturated activity in the network as the mean degree is changed across a fairly narrow band of values.
Experimenting and exploring with this software, I made several general observations about the behavior of these networks. Most obvious and immediately apparent was confirmation that each network, regardless of size, moves from a regime of absolute quiesence (no nodes spiking) to one of maximum constant homogeneous activity (all nodes spiking all the time) as one of several parameters is increased monotonically. Except when other parameters are set to extreme values (e.g. probability of edge = 0), each of the following parameters invoked this phase transition behavior as it is modulated accordingly: mean degree (or, equivalently, probability of an edge between any two nodes), size of stimulus delivered in response to an action potential, threshold to fire, and to a lesser extent (i.e. tighter constraints are necessary on other parameters) the decay rate of node voltage.
I also observed that each of the networks, regardless of configuration, is extremely sensitive to changes in these parameters. Not only do we enter or fall out of quiescent or seemingly epilleptic states quickly, but also one may notice significant qualitative changes in the type of patterns being displayed by the system for given parameter vectors. For instance, simply by changing the probability of edge presence by 1% in a 30 node network from 14% to 15% we see our spiking pattern go from complex and possibly even chaotic to very simple and repetitive. This observation is significantly repeatable according to a limited number of observations made thus far.
System under investigation
The specific formulation of the underlying dynamics and chosen representation of the neural networks explored in this and earlier work can be found here.
Methods
Extending the spiking neural network software framework which I constructed previously, I have added a (currently non-interactive) capacity to measure entropy of network behavior in time as well as time shifted mutual information between neural spike bit streams of pairs of neurons in the network.
In all networks, to control the number of variables, I started all neurons in the network spiking on the initial time step of every trial. All networks were configured with a spike threshold at each node of 1 and to deliver a stimulus (i.e. increase in non-dimensionalized voltage) of .5001 to any neurons on the receiving end of an edge originating from that node. The decay constant was different for each of the two types of experiments described below.
Exploring and comparing entropy of networks
To begin to quantitatively explore the range of possible behavior in these networks, I wrote a routine to calculate the entropy of the network over time. Specifically, my code treats each N-bit binary block (where N is the number of nodes in the network) as a possible element of an alphabet. Then at each time step the network generates a single symbol composed of the outputs of each of its constituent nodes at that timestep. Taken over time, Shannon entropy can be calculated using the standard formula.
I found six node networks to be of an ideal size which was manageable but through which complex and interesting behaviors could still maninfest.
A batch of 100 trials of such networks with random connectivity between 25% and 75% (i.e. the probability of an edge existing between any two nodes) was run, each for 3000 time steps with the first 50 time steps disregarded as transient. Entropy was both maximized and minimized among these trials and the resulting patterns were noted and analyzed.
A second set of experiments were run focusing instead on the transients. In these trials, only the first 40 timesteps were observed. Entropy was calculated and max/minimized for these timesteps across 8,000 trials.
Neurons in these trials uniformly had a decay/leak constant of .05. This is the rate at which voltage disipates out of the neuron when the neuron is not at its resting potential.
Exploring shifted mutual information between neurons/nodes in a network
The second category of experiments employed in this work focused instead on relationships between individual neurons in a given network.
Given a network of four or five neurons, shifted mutual information was calculated in the following way. For all possible pairwise combinations of neurons in the network, the standard mutual informaiton formula was applied to the two associated spike train bit streams recorded during a trial. Then the two bit streams were shifted temporally with respect to one another in both directions up to four time steps and the resultant time-shifted streams were then passed to the same mutual information calculation routine. This resulted in an NxNxT three dimensional matrix of values, where T is twice the maximum shift in any direction plus one (for the zero shift). Any time slice along the T axis in this matrix produces a NxN symetric matrix. Maximums in these matricies were inspected.
Initial observations of shifted mutual information in randomly constructed networks suggested the possibility that structural patterns in the the connectivity of the networks were reflected in the behavior of the associated neurons. To investigate this further two specific networks were designed and explored (explained below).
Neurons in these trials uniformly had a decay/leak constant of .01, much smaller than above, which aided in designing simple networks that had predictable (i.e. more linear) behavior over time.
Results
Network entropy
Persistent pattern analysis
Below I present four screenshots of the interface representing networks and behaviors for two of the hundred networks tried which had relatively high entropy (top) and relatively low entropy (bottom). The first two cases are representative of the two general ways in which I observed networks to obtain better than average entropy. Specifically, the first way was to produce spike bit streams containing a relatively large number of different symbols out of the 2^6=32 possible in the alphabet with variable probability density function shapes. The second way was for networks to produce a few patterns which appeared almost with uniform probability, almost always in the form of a small cycle (3 or 4 unique patterns in series typically) Interestingly, it appeared, at least in my trials that 6 node networks of this variety were unable to both maximize diversity as well as homogeneity in the frequency distributions of the symbols.
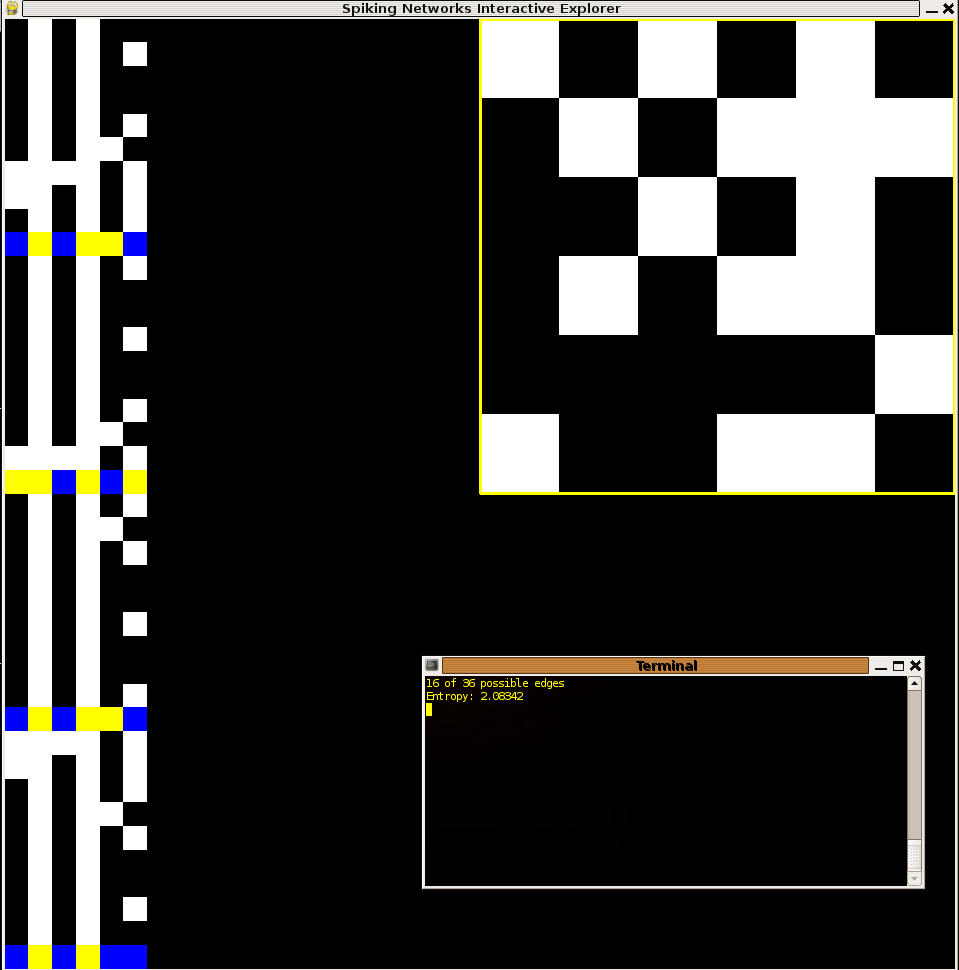


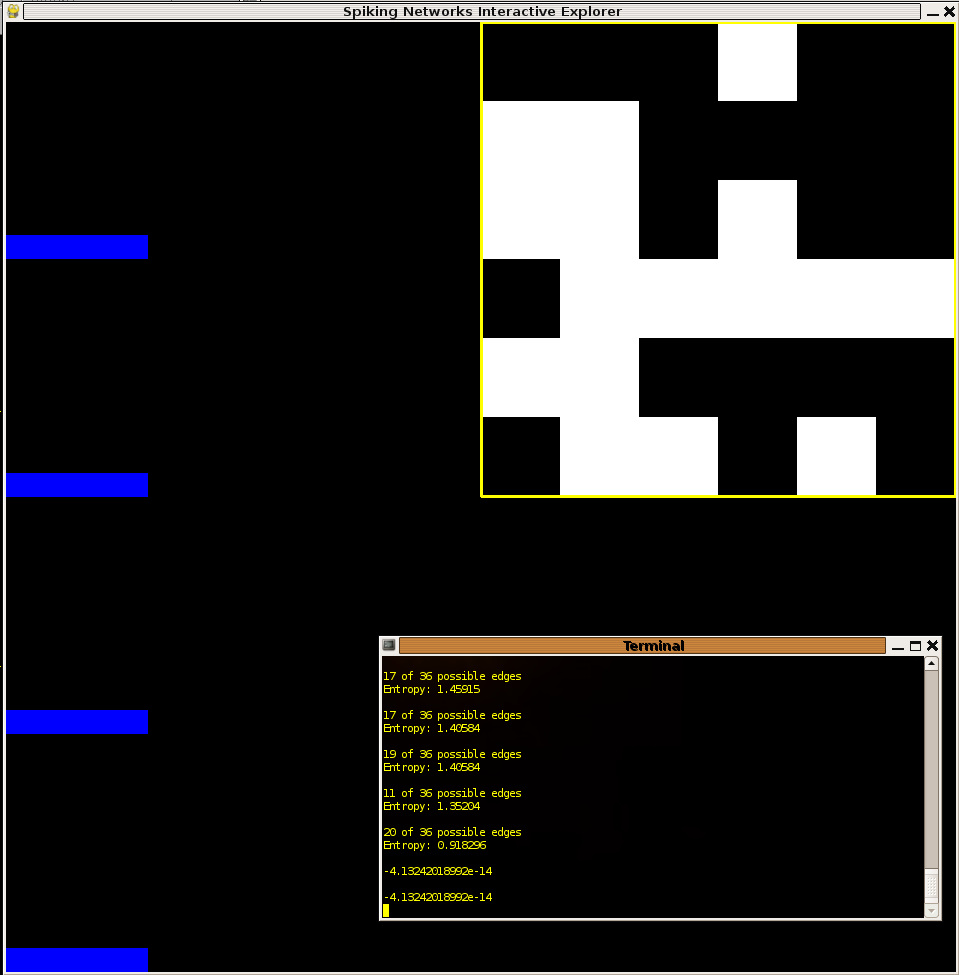
Figure 1: See this description to understand the interface presented. Top left:. Large entropy produced through diverse bitstreams (diversity mostly contributed from the last neuron). Top right: Large entropy produced through cyclic (specifically 3-cycle) behavior. Bottom: Small entropy resultant from homogenous output. Initial conditions for all networks: every node spiking.
Recall that entropy = sum(-p*log2(p)) where the sum is across a vector of probabilities each corresponding to the probability a particular symbol is seen at any time step. Below I present a MATLAB plot of p vs. -p*log2(p) from 0 to 1 where log2(p) is log base-2. Graphically then we see that since a higher sum is achieved either by having many elements in the vector to sum over or by having those elements be fairly uniformly represented (thus increasing the number of probabilities which fall near the maximum of the graph), the two strategies each make sense.

Figure 2: MATLAB plot of p vs. -p*log2(p) from 0 to 1 where log2(p) is log base-2.
Transient pattern analysis
Although most times in calculating probability distributions it is advisable to take the maximum number of samples and throw out any "transients" of the system being studied, it seems conceivable that transient behavior could be useful within the context of a nervous system which may rely on some sub-networks to respond quickly and with behaviors which generate information rich data in a timely manner. It is with this idea in mind that I ran a second set of experiments to study the behavior of network configurations which maximize entropy over the first 40 samples. Since the sample size in each trial was so small I was able to run almost two orders of magnitude more trials. It is perhaps for this reason that the maximum entropies delivered were of about a bit more than those in the persistant case. Below I present two examples of networks with high entropy transient behavior. Again we see the dichotomy discussed in the persistant case above. It is interesting to observe that many of the networks with the highest entropies "died out" after only 20 or 30 time steps.
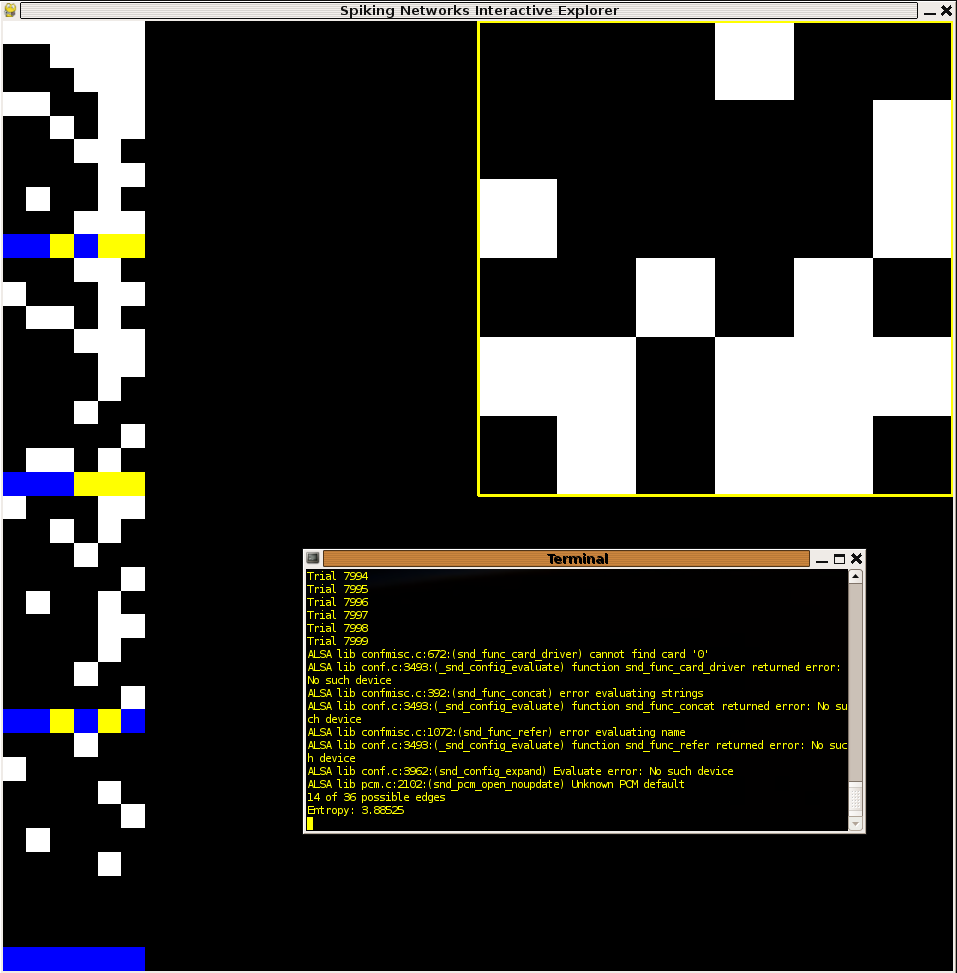
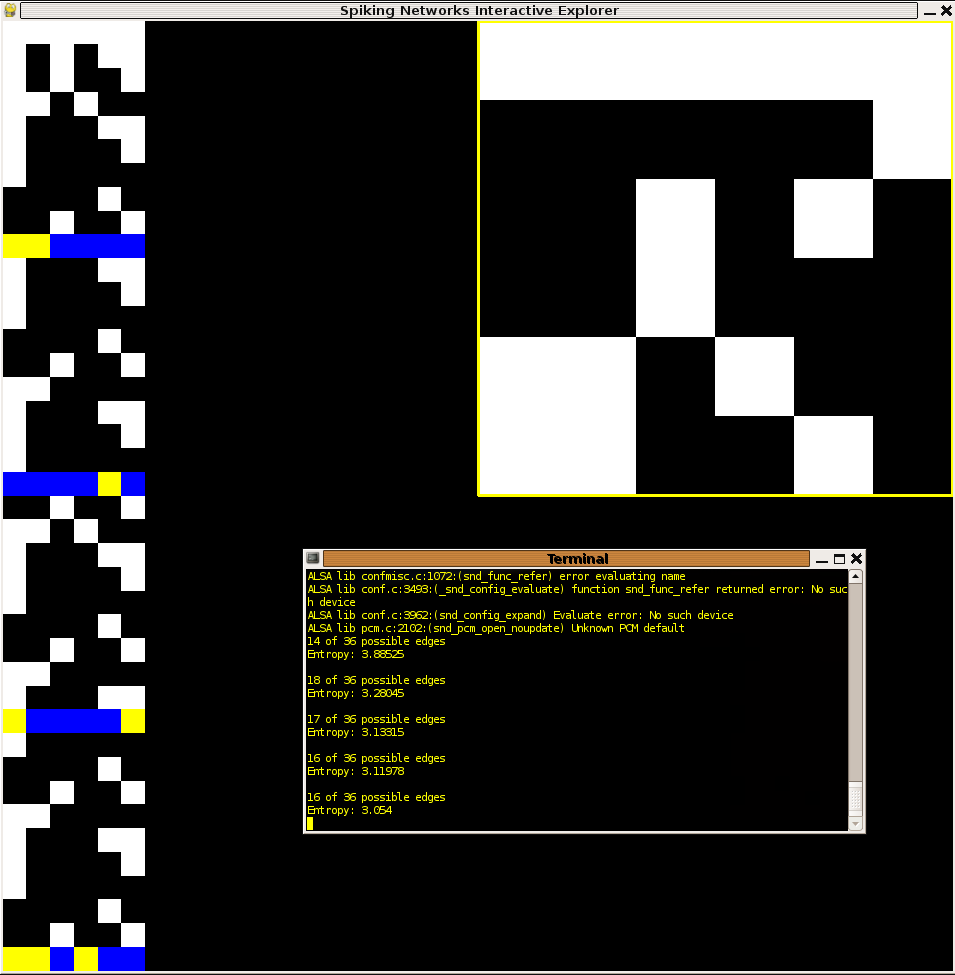
Figure 3:Networks with relatively large entropy in the transient timesteps (first 40). Note in the left network how activity dies out before even reaching 40 timesteps. This network exhibited the maximum entropy of all networks tested: 3.88. Initial conditions for all networks: every node spiking.
Shifted mutual information between neurons
Shifted mutual information, as described above, indicates quantatatively the degree to which a spike train recording of one neuron may be indicative of what to expect in the recording of another neuron. The temporal shifting in this measurement gives us a sense of the temporal relationship between the two neurons.
Since initial measurements in randomly constructed networks suggested the possibility that structural patterns in the the connectivity of the networks are reflected in the behavior of the associated neurons, I constructed two specific networks to study this idea.
Four neuron network
This network, presented graphically in the screenshot below is the simplest possible design which generates persistent activity that "trickles" its way down a one way chain of neurons. In this consruction two neurons mutually and self excite, leading to constant spiking in both. One of the neurons also exclusively excites a third neuron. Since it would not be informative to compare any spike train with one which has no pattern to it (i.e. spiking all the time), it is necessary to introduce a fourth neuron to the network. The simplest possible way to introduce this neuron to the group is to add it as a receiver of stimuli coming from the third neuron.

Figure 4: Designed four node network exhibiting behavioral reflection of structural connectivity through measurements of shifted mutual information. We will refer to neurons A,B,C,D in order up/right on the adjacency matrix. (so A/B are fully connected) Note that the adjacency matrix reads: from column, to row.
The table below sumarizes the results of the shifted mutual information calculation.
| Node1 | Node2 | Time shift | Mutual information |
|---|---|---|---|
| C | D | -1 | ~.197 |
| C | D | 2 | ~.197 |
| C | D | otherwise | ~.07 |
| All other combinations | All shifts | ~0 | |
Table 1: Note Time shift is with respect to Node1. So in the first row we are comparing the output of neuron C shifted back one time step to neuron D without a shift.
What we see here is that the activity of neuron C one time step ago is quite indicative of what neuron D is doing in the current time step. This, clearly, is a result of the causal structure of the network. (C->D) One might expect from this analysis that neuron D two time steps in the past is equally indicative of what C is doing now, but this is simply an artifact of the cyclic nature of the process and not reflective of the causal structure of the network. This shows that one must be very careful when inferring causal structure with this sort of measurement.
Five neuron network
To see if this result holds when another neuron is added to the network, I constructed and tested such a network presented below.

Figure 5: Designed five node network, which is the same as the four node network with an extra node being stimulated by the last node in the chain.
Again a table summarizes the (slightly more complex) results.
| Node1 | Node2 | Time shift | Mutual information |
|---|---|---|---|
| C | D | All shifts | same as above |
| D | E | -1 | ~.126 |
| D | E | otherwise | ~.006 |
| C | E | -2 | ~.06 |
| C | E | 1 | ~.06 | C | E | otherwise | ~.022 |
| All other combinations | All shifts | ~0 | |
Table 2: Shifted mutual information in a five node network.
Beyond what we saw before between C and D (which is repeated here since adding E doesn't causually effect anything else in the network) we see in this result that there is a peak in mutual information when D is shifted back one timestep with respect to E and a smaller peak when C is shifted back two time steps with respect to E. This confirms what we saw above in the same way discussed there. Furthermore we note that the peak mutual information between D and E is larger than between C and E. This result is discussed further below in the context of the data processing inequality for Markov chains.
Further thoughts
Recall that Shannon entropy will be maximum when every symbol out of an alphabet is present in a sample distribution with equal probability. As presented above, I have found that both in my persistant and transient trials, the behavior of networks which maximize entropy relative to other networks tested fall into two main categories: those which contain many patterns but in unequal probabilities or those which have equal probabilities but few patterns. This result is compelling food for future research. One particularly pressing question is whether the trend seen of a failure to use both strategies for maximizing entropy is indicative of a fundamental limitation on these small networks or whether there are in fact some specific networks which are able to close the gap on entropy maximization.
Just as the experiments exploring mutual information in the designed four node network gave compelling evidence that structure in these sorts of networks may be readily reflected in the spike trains coming out of the network, the experiments with the five node network are suggestive of a further fact. Namely that the data processing inequality which is universally true of Markov chains may also be true in some form for some types of spiking neural networks. That is to say if there is a one way chain of causal effect A->B->C (where A, B and C are neurons), the information in the behavior of A is more informative of that of B (and vice-versa) than it is of C. The idea is intuitive but more work is necessary to show conclusively that it holds in all cases in spiking neural networks.
Next Steps
Finally, I will conclude with a few brief ideas for follow-up development and research.
2D Block entropy
Response to input
Network "moods"
Mapping patterns in structure to patterns in behavior
Behavior vs. "function"
Since ultimately what is important is to study patterns of these networks in time, it may make sense to extend the analysis of entropy to "2D" block entropy. That is not only to look at the N-block which is output of all nodes at any given time step, but also to look at the distribution of NxK blocks where K is a number of time steps.
Clearly another interesting and important topic which would add depth and complexity to this research would be to study how various networks respond to different sorts of input. Do some networks respond almost identically to different inputs while others respond in wildly different ways? Are there certain patterns of connectivity which set these two sorts of networks apart?
To take the last step even further, for a given network, will that network respond the same way to a given input no matter what state the network is in upon receiving hte input, or does the network exhibit "moods" which make it less predictable but perhaps more computationally powerful in some contexts?
Ultimately I think it would be extremely compelling to find consistent mappings betwen structural patterns of connectivity in networks and the resultant behavior. For simple pattern classes with known associated behavioral regimes, how do connecting two ore more of these networks together effect the overall behavior?
One last question which reminds us of the role of these networks in the success of an organism which utilizes them is what role certain low level behavioral patterns observed play in providing useful functionality to the organism.
Code
Code is available here. Previously I listed some steps to take to get the other code running. Steps here are identical, replacing the final command with "python SpikeInformation.py"