How does evolution produce sophisticated emergent computation in systems composed of simple components limited to local interactions?

In our work, we use genetic algorithms to evolve cellular automata to perform computational tasks requiring global information processing. We then analyze both the evolutionary process and the emergent behaviors of the evolved cellular automata that give rise to their computational abilities. This way, we hope to find answers to the above question. This page presents a short introduction to the evolving cellular automata framework, including some results. Please see the papers on evolving cellular automata with genetic algorithms for more details about this project.

Genetic Algorithms

Genetic algorithms (GAs) are stochastic search methods inspired by biological evolution. They are also widely used as simple models of evolutionary processes. A GA maintains a population of "individuals", often encoded as bit strings (the "genetic" material). These individuals can, for example, represent candidate solutions to some given problem, or "agents" living in some artificial environment, or parameter values for an optimization problem, etc. Starting out with a random initial population, the GA then "evolves" this population of individuals by means of (artificial) selection and reproduction with variation as follows.

First, each individual is assigned a fitness value. This fitness value reflects how well the candidate solution that this individual represent solves the given problem, or how well the agent this individual represents manages to make a living in its artificial world, etc. In other words, the "better" the individual is, the higher its fitness value will be. Individuals are then selected at random according to their fitness values, where a higher fitness (relative to the population average) means a higher chance of being selected (possibly multiple times). A new population of offspring individuals is then created by randomly "mating" the selected individuals. In this process, recombination operators like crossover (mixing the "genetic" material of the selected individuals) and mutation (randomly changing some of the "genetic" material of an individual) are applied to create offspring that are genetic variants of their "parents".

This process of assigning fitness values, selecting individuals, and creating offspring with genetic variation is then repeated for many "generations". This way, better and better individuals are evolved by (re)combining partial solutions of parent individuals and by finding innovations through mutations, all driven by the selection process. In this sense, a GA mimics biological evolution.

Cellular Automata

Cellular automata (CAs) are dynamical systems that are discrete in state, space, and time. In the simplest case, a CA consists of a one-dimensional lattice of identical cells, each of which can be in one of a number of states. Again in the simplest case, let's say each cell can be either white (0) or black (1). At each time step, all cells in the lattice update their state simultaneously by using a fixed update rule which is the same for each cell. This update rule takes as input the local neighborhood configuration of a given cell (i.e., the current states of the cell and its r neighbors on either side), and returns the new state of the cell depending on this local neighborhood configuration. Thus, this update rule can be represented as a lookup table which lists all possible local neighborhood configurations together with the corresponding new cell states.

Different update rules (or lookup tables) give rise to different kinds of CA dynamics when this update rule is iterated over time, ranging from fixed point or simple periodic behavior to highly complex or even "chaotic". The particular behavior of a CA can be visualized in a space-time diagram, in which the CA lattice configurations are plotted over time, usually starting with a random initial configuration.

Computational Tasks

We can ask whether there exist CAs (i.e., particular lookup tables) that can perform computations. A computation here will mean that an input is encoded in the form of an initial configuration and the intermediate time steps while iterating the CA then transform this input to some output encoded in the form of a lattice configuration after a certain (fixed) number of time steps. Thus we can ask whether there exist CAs that are capable of transforming certain classes of inputs to corresponding classes of outputs.

One example of such a task is density classification. For this task the CA has to decide, given a random initial configuration of black and white cells, whether there are more black cells or more white cells in this initial configuration. When there are more black cells, the CA should settle down to an all-black configuration (in at most some number M of time steps), otherwise it should settle down to an all-white configuration. Note that this is a non-trivial task for a CA, since the existence of a majority of black (white) cells is a property of the lattice as a whole, while each cell in the CA can communicate only locally.

Evolving CAs with GAs

Given a computational task such as density classification, we can now use a GA to try to evolve CAs that are capable of performing this task. We use one-dimensional CAs with two states (white and black), where the local neighborhood of a cell consists of the cell itself and the three neighboring cells on either side, i.e., a local neighborhood of seven cells. This gives rise to a lookup table with 2⁷=128 entries. Since each of these entries can have either a 0 or a 1 for the cell's next state, there are 2¹²⁸ possible CA lookup tables. This is the size of the space that the GA will be searching through.

The GA maintains a population of 100 individuals (representing CA lookup tables). The initial population is created at random. The fitness of an individual (CA) is determined as follows. Each CA in the population is given a random set of 100 initial configurations (ICs). The fraction of these ICs on which it gives the correct answer is its fitness. So, if the CA settles down to the correct answer state (all-white for a majority of white cells in the IC or all-black for a majority of black cells in the IC) on 75 of the ICs, its fitness is 0.75. The GA is run for a total of 100 generations.

Some Results

The figure below shows the result of one particular GA run on the density classification task. The diagram in the top-left corner shows the best fitness in the population over time. The arrows indicate five different generations (12, 13, 16, 18, and 100) during the evolution. The five space-time diagrams show typical behaviors of the CAs that were the best individual (i.e., had the highest fitness) in these respective generations.

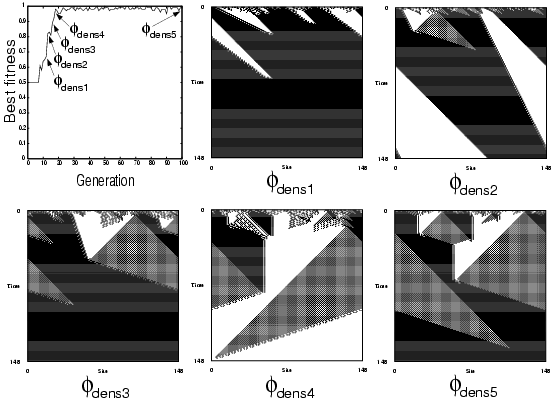
Both the dynamics and the evolutionary history of these CAs can be analyzed in terms of the emergent pattern formation that occurs in these CAs (in particular the white, black, and checkerboard (gray) regions and the boundaries between them). For this analysis, we use the computational mechanics framework. These analyses lead to a better understanding of (the evolution of) emergent computation in CAs, and even to a way of quantitatively predicting (changes in) the computational performances (fitness values) of these evolved CAs.

For a more detailed overview of the EvCA framework and the results of both evolving CAs with GAs and the subsequent analyses, please see the various papers by our group.