![(
|{1 - 2xn 0 ≤ xn ≤ 1
x = f (x ) = 2x - 1 1 < x ≤ 32 x ∈ [0,1] .
n+1 n |( n 3 32 n 3 n
3 - 3xn 3 < xn ≤ 1](Week70x.png) | (1) |
Construct a Markov partition for this map, as follows.
- Plot xn+1 versus xn.
- Find the monotone pieces of f(x) by determining the locations of its extrema.
- Show that the segments defined by the ends of the interval and these locations form a Markov partition.
- Give the Markov chain induced by this partition.
- Calculate the asymptotic state distribution pV (∞) for the Markov chain.
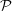 Markov for the logistic map at the parameter setting
where 2 bands merge into 1 band. Analyze a generating partition for this same situation, as
follows.
Markov for the logistic map at the parameter setting
where 2 bands merge into 1 band. Analyze a generating partition for this same situation, as
follows.
- Consider the binary partition of the interval
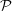 gen = {0 ~ (0,
gen = {0 ~ (0,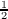 ),1 ~ (
),1 ~ (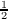 ,1)}. Label the transitions
in last week’s Markov chain with the symbols observed using
,1)}. Label the transitions
in last week’s Markov chain with the symbols observed using 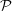 gen when making transitions
between Markov partition elements.
gen when making transitions
between Markov partition elements.
- Show that the resulting representation is a unifilar hidden Markov process.
- How many internal (Markov) state sequences map onto the observed sequence of all 1s? Are there any other examples of many-to-one mappings of state sequences onto observed sequences?
- States are equivalent if the sets of sequences that follow from them are the same. Give a hidden Markov chain with fewer states than the one just constructed by identifying states that are equivalent in this sense.
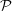 gen = {0 ~ (0,
gen = {0 ~ (0, ),1 ~ (
),1 ~ (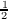 ,1)}?
,1)}?
- Show that the partition
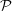 = {A ~ (0,
= {A ~ (0,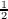 ),B ~ (
),B ~ (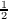 ,1)} is a Markov partition and give the induced
Markov chain.
,1)} is a Markov partition and give the induced
Markov chain.
- Let x* be the largest of the two inverse iterates of
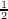 : x* = max{f-1(
: x* = max{f-1(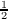 )}. Observe the logistic
map with the binary partition
)}. Observe the logistic
map with the binary partition 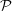 bad = {1 ~ (0,x*),0 ~ (x*,1)}. Give the hidden Markov chain
which this partition induces. As above, this is a labeling of Markov chain’s transitions according
to
bad = {1 ~ (0,x*),0 ~ (x*,1)}. Give the hidden Markov chain
which this partition induces. As above, this is a labeling of Markov chain’s transitions according
to 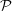 bad.
bad.
- Is this hidden Markov chain unifilar?
- Give a complete summary of the state sequences (over {A,B}) that map onto the all-1s sequence.