Covering Lecture Notes.

1. Analyze the following period-3 process:
   1. Give the labeled transition matrices for a hidden Markov process that endlessly repeats the 3-letter word 101.
   2. Assume that you do not know what state the internal Markov chain is in. Without this knowledge, we can assume the process is in one or another of the internal states with equal probability. What state or states is the process in, if you now measure a s = 1? Give the state distribution in this case. What state or states are you in, if you then observe s = 0?
   3. Calculate the sequence probabilities Pr(s^L) for sequence lengths L = 1,2,3,4.
2. Analyze the biased coin process:
   1. Write down the two-state Markov chain transition matrix for a process that generates Heads with probability p > 1∕2 and Tails with probability 1 - p.
   2. At a given length, which sequences have the lowest probability?
   3. At a given length, which sequences have the highest probability?
   4. Are the latter what you will observe as typical realizations of the biased coin process? If yes, why? If not, what other sequences would you typically observe?
3. Show that the Even Process is not a finite Markov chain. Recall that the Even Process is defined by two labeled-transition matrices:

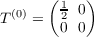   (1)

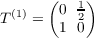   (2)

   You can do this by constructing Markov chain approximations and showing that one has to take the limit to correctly describe the sequence distribution of the Even Process, resulting in an infinite number of Markov chain states.

4. Give the Markov partition for the logistic map (x_n+1 = rx_n(1 - x_n)) where two bands merge to one:
   1. Calculate the parameter value where the band merging occurs. Show how you did this.
   2. Calculate the intervals for the Markov partition 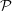= {…,(d_i,d_i+1),…}. How many intervals are there? Is this the smallest number possible?
   3. Give the labeled directed graph that describes the Markov chain for the map observed with this partition.
   4. Calculate the asymptotic state distribution for the state of this Markov chain.

Homework due one week after being assigned.